電界(電場)を理解するためには、クーロン力やベクトルの足し算引き算の知識が必要不可欠です。こちらについては、以前の記事(クーロンの法則)でまとめているのでご覧ください。
電荷が周囲におよぼす力
ある空間(厳密には真空中)にq0とqの電荷の間に働くクーロン力は、クーロンの法則により以下の式で表されます。
$$
\begin{align}
F\bigl[N\bigr]&=k\Biggl[\frac{N×m^{2}}{C^{2}}\Biggr]×\frac{q_0\bigl[C\bigr]×q\bigl[C\bigr]}{r^{2}\bigl[m^{2}\bigr]} \\\\
&=q×k\frac{q_0}{r^{2}} \\\
&=q×E
\end{align}
$$
ここで、Eはq0の電荷が周囲に及ぼす力(電界)と定義されます。そのため、qにかかるクーロン力は、「q0の電荷が周囲に及ぼす力をqが感じ取っている」と解釈することができます(図1)。
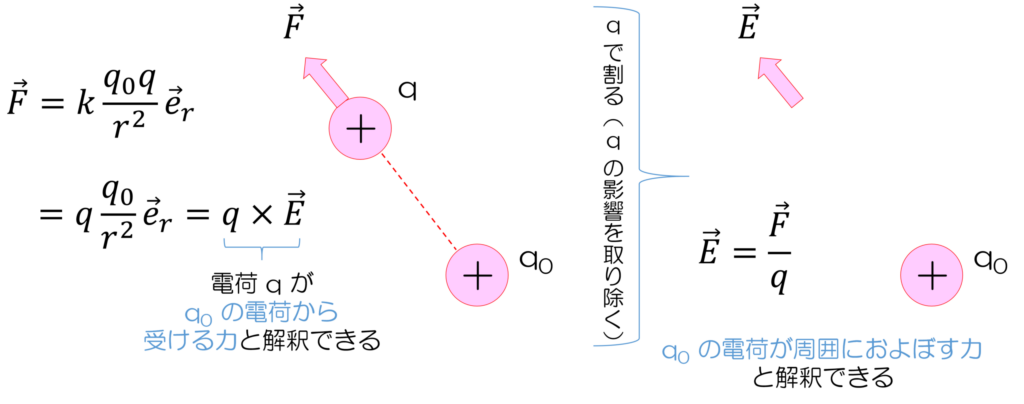
図1 q0の周囲の電場測定
ある点にq0の電荷を置き、様々な点に電荷qを置きクーロン力を調べ、qで割り・・・という作業を永遠と行うと、図2のような分布が完成します。
これをq0の電荷が発する 電界 または 電場 と呼んでいます。
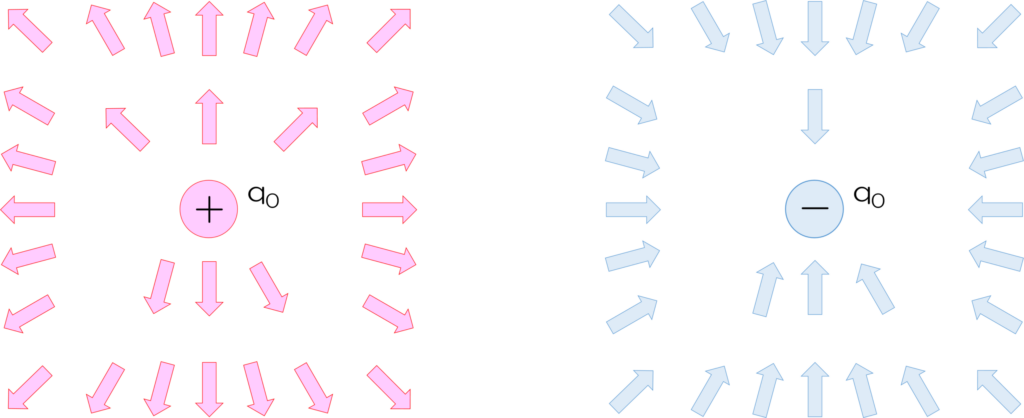
図2 電荷がまわりにおよぼす力
また、これを式に表すと以下のようになります。
$$
\vec{F}=q×k\frac{q_0}{r^{2}}×\vec{e}=q×\vec{E} \\\
$$
$$
\vec{E}=\frac{\vec{F}\bigl[N\bigr]}{q\bigl[C\bigr]}
$$
この式から、電界の単位は[N/C]になりそうですが、一般的には [V/m] になります。
このことについては、静電ポテンシャルについて理解していなければならないので、一旦スルーし別の機会に解説したいと思います。
重ね合わせの原理
先ほどの式を見てみると、電界はベクトル量(図2では、プラスの電荷は外向き、マイナスの電荷は内向き)で表されているため、クーロン力のときと同様にベクトルの足し算と引き算が適用されます(図3)。
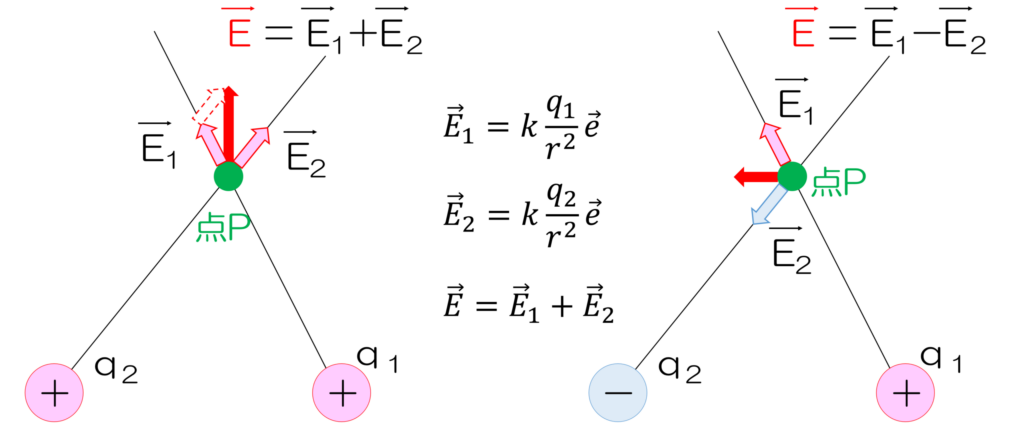
図3 電界の計算
これをもう少し、カッコよく書くと以下のようになります。
$$
\vec{E}\bigl[V/m\bigr]=\vec{E}_1\bigl[V/m\bigr]+\vec{E}_2\bigl[V/m\bigr]+\vec{E}_3\bigl[V/m\bigr]+・・・+\vec{E}_N\bigl[V/m\bigr]
$$
$$
\vec{E}=\sum_{i=1}^{N}\vec{E}_i\bigl[V/m\bigr]
$$
まとめ
- 電界Eはq0の電荷が周囲に及ぼす力として定義されます
- 電界Eはベクトル量なので、足し算や引き算が可能です。
- 電界Eの単位は[N/C]と勘違いされやすいですが、一般的には[V/m]になります。



