スカラー量とベクトル量
物理量を大きく分けるとスカラー量とベクトル量に分かれます。スカラー量とは量の大きさのみを表すものであり、ベクトル量は量の大きさと向きを表します。
スカラー量の例:長さ、質量など
ベクトル量の例:速度、風速など
どちらも足し算と引き算が可能であるという特徴があります。
ベクトルの足し算と引き算
スカラー量もベクトル量も足し引きが可能ですが、ベクトル量の場合は向きが存在するため、少しだけ複雑になります。
ベクトル\(\vec{A}\) とベクトル\(\vec{B}\) の足し算は、図1のようにベクトル\(\vec{A}\) の終点とベクトル\(\vec{B}\) の始点をつなぎ、これらを結びます。
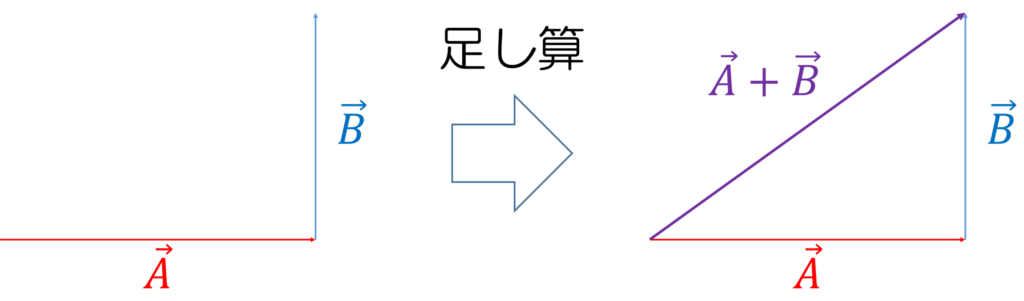
図1 ベクトルの足し算
引き算の場合は、マイナスのベクトルを足すという考え方で計算を行います。今回の場合は、図1で上向きだったベクトル\(\vec{B}\) が、マイナスとなるため、向きが180度方向転換します(図2)。
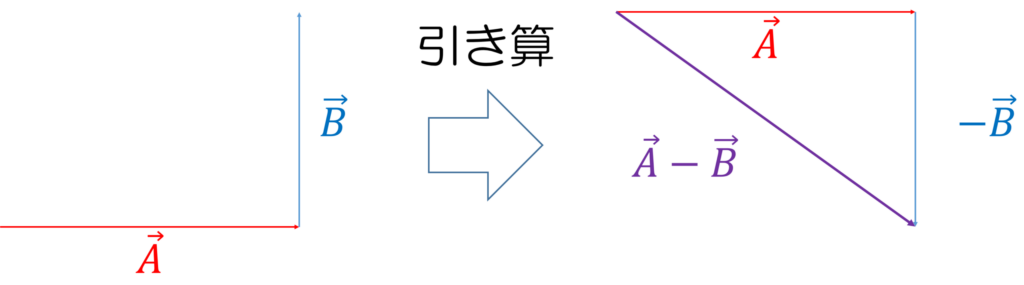
図2 ベクトルの引き算
クーロンの法則
クーロンは1785年に、次のような法則を発見しました。
2つの電荷間に働く力の方向は、それらを結ぶ直線上にあり、電荷間の符号が同じ場合は反発力、符号が異なる場合は吸引力となります(図3)。このとき電荷間に働く力の大きさは、電荷の積に比例し、電荷間の距離の2乗に反比例します。
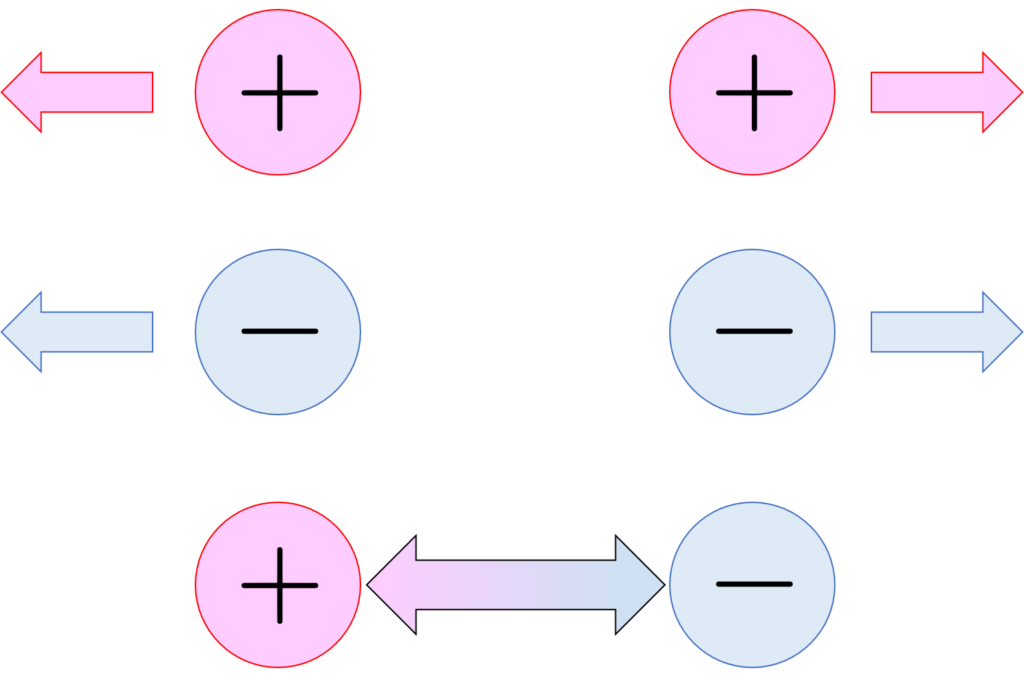
図3 クーロン力
これを定数kを使って式に表すと、以下のようになります。
$$
F\bigl[N\bigr]=k\Biggl[\frac{N×m^{2}}{C^{2}}\Biggr]×\frac{Q_1\bigl[C\bigr]×Q_2\bigl[C\bigr]}{r^{2}\bigl[m^{2}\bigr]}
$$
ここで、Fはクーロン力の大きさ、kはクーロン定数、Q1とQ2電荷量の大きさ、rは電荷間の距離を表しています。また、[ ]で囲われているのは、それぞれの要素の単位になります。
これをクーロンの法則といい、電荷間に働く力を クーロン力(静電力)といいます。
問題に「電荷間の距離は30cmである。」などと書かれていた場合は、距離の単位を
cmからmへ変換する必要があるので注意してください。
また、この式は力の大きさを表しているため、スカラー量です。クーロン力は大きさに向き(反発力であれば外向き、吸引力であれば内向き)が加わっているので、ベクトル量で考えなければなりません。
力の向きを考慮したベクトル量は、以下の式で表されます。
$$
\vec{F}\bigl[N\bigr]=k\Biggl[\frac{N×m^{2}}{C^{2}}\Biggr]×\frac{Q_1\bigl[C\bigr]×Q_2\bigl[C\bigr]}{r^{2}\bigl[m^{2}\bigr]}×\vec{e}_{12}
$$
\(\vec{e}_{12}\) は、大きさが1になる単位ベクトルと呼ばれるものです。
そのため、数値的な計算結果は同じになります。
力の向きを考慮したクーロン力はベクトル量のため、足し算や引き算が可能になります。
重ね合わせの原理
クーロン力はベクトル量であるため、足し算や引き算を行うことができます。これは、複数の電荷が存在しているとき、1つの電荷にかかるクーロン力を考えるときに便利です(図4)。これを式で表すと以下のようになります。
$$
\begin{align}
F&=k\frac{Q_1(Q_2+Q_3)}{r^{2}} \\\\
&=k\frac{Q_1Q_2+Q_1Q_3}{r^{2}} \\\\
&=k\frac{Q_1Q_2}{r^{2}}+k\frac{Q_1Q_3}{r^{2}} \\\\
&=F_{12}+F_{13}
\end{align}
$$
このように複数の電荷がある場合は、単純なクーロン力の足し合わせで計算することができます。
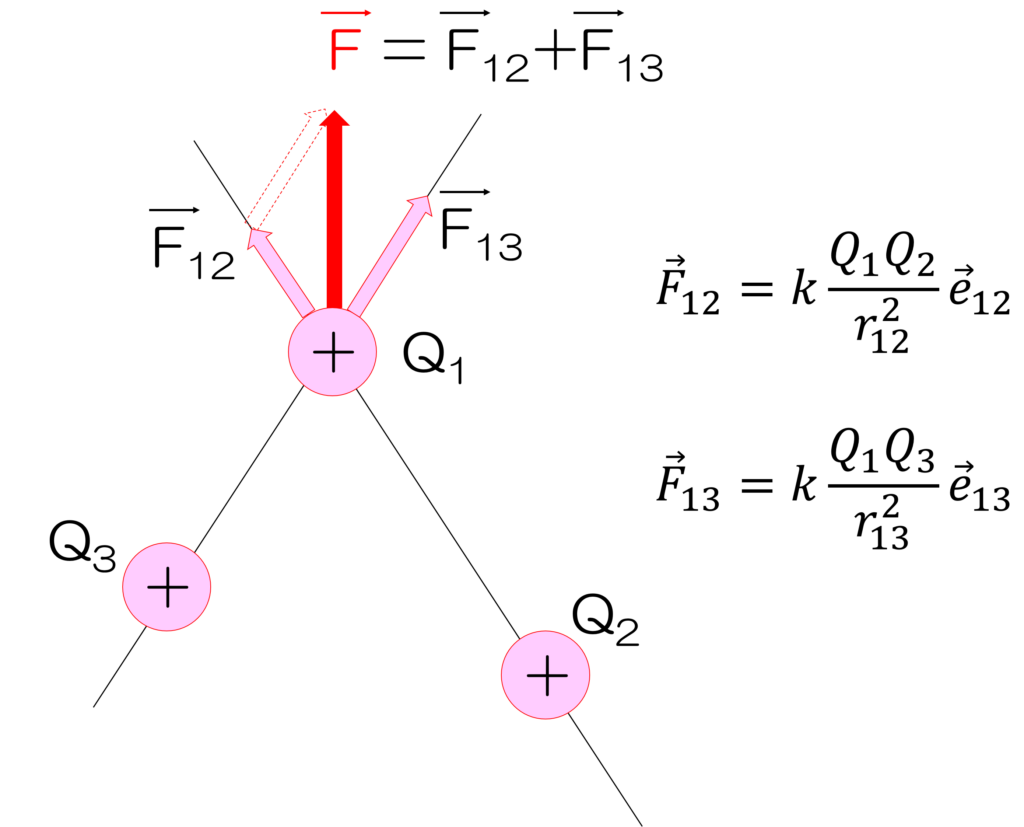
図4 クーロン力の重ね合わせ
これをもう少し、カッコよく書くと以下のようになります。
$$
F\bigl[N\bigr]=F_1\bigl[N\bigr]+F_2\bigl[N\bigr]+F_3\bigl[N\bigr]+・・・+F_N\bigl[N\bigr]=\sum_{i=1}^{N}F_i\bigl[N\bigr]
$$
ただし、診療放射線技師国家試験では、クーロン力の大きさを問う問題しか見たことがないので、(おそらく)重ね合わせの原理までは出題されないのかなと思います。
まとめ
- クーロン力は、電荷間の符号が同じ場合は反発力、符号が異なる場合は吸引力となります。
- クーロン力はベクトル量なので、足し算や引き算が可能です。
- その他、式が出てきたときには、その要素と単位を必ず確認して下さい。
値をそのまま代入した場合、計算が合わなくなる可能性が非常に高いです。



